• Research questions/goals: Currently, our focus is to elucidate the mechanisms that allow for persistent Epstein-Barr virus (EBV) infection in humans using mathematical modeling and computer simulation.
• Current main results and/or publications: Hawkins JB, Delgado-Eckert E, Thorley-Lawson DA, Shapiro M. The cycle of EBV infection explains persistence, the sizes of the infected cell populations and which come under CTL regulation. PLoS Pathogens. 2013 Oct;9(10):e1003685. doi:10.1371/journal.ppat.1003685
• If you are interested in this topic, please watch the following video of a talk I gave at the 3rd Workshop and Conference on "Modeling Infectious Diseases" organized by The Indian Institute of Mathematical Sciences (IMSc), Chennai, India, November 2015. 
• Funding: New collaborations and facets of this research line were funded by a Marie Curie International Research Staff Exchange Scheme grant from the European Commission, which started in May 2013. 
• Collaborators: Dr. Michael Shapiro of the Francis Crick Institute, London, UK, Prof. David Thorley-Lawson of Tufts Medical School, Tufts University, Boston, USA, and Dr. Jared Hawkins of the Laboratory for Personalized Medicine at Harvard Medical School, Boston.

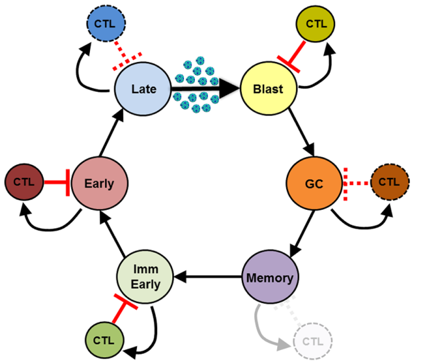
Many years of scientific research have led our collaborators to propose a cycle of replication for the Epstein-Barr virus (EBV) in the human body. Indeed, experimental evidence suggests that the virus takes advantage of the physiological cycle of B cells. We have tested some of the logical consequences of this model using mathematical modelling and computer simulation. We were able to derive consequences concerning the differences in the pathology of EBV infection between individuals in a population of EBV positive persons. It turns out that the differences predicted by the model are actually observed in the human population! This is a strong argument in favor of the validity of the “cyclic pathogen model” of EBV infection. Find out more.